Compilation

Planche : 2

A: Qu’est-ce que compiler ?
B: Machine abstraite.
C: Compilation de PCF.

Presque un ordinateur

Programmer l’ENIAC (1946), c’est connecter des câbles.

Un peu plus tard (Iris 10 010, 1967)

Programmer un ordinateur, c’est entrer un programme en mémoire.

Un ordinateur

Par définition ou presque (machine de Von Neumann), un ordinateur est :

Une machine « universelle ».
Composée d’une unité de contrôle et d’une mémoire.
L’UC lit (et exécute en séquence) un programme à partir de la mémoire.
Le programme est une séquence d’instructions élémentaires :
- Lire/Écrire une case de mémoire.
- Additionner le contenu de deux cases de mémoire.
- Lire (et exécuter) une instruction qui n’est pas la suivante.
- etc.

Entrer un programme en mémoire

Il s’agit d’un détail technique. Par exemple…

Années 80, « amateur » fauché		Aujourd’hui, assembleur

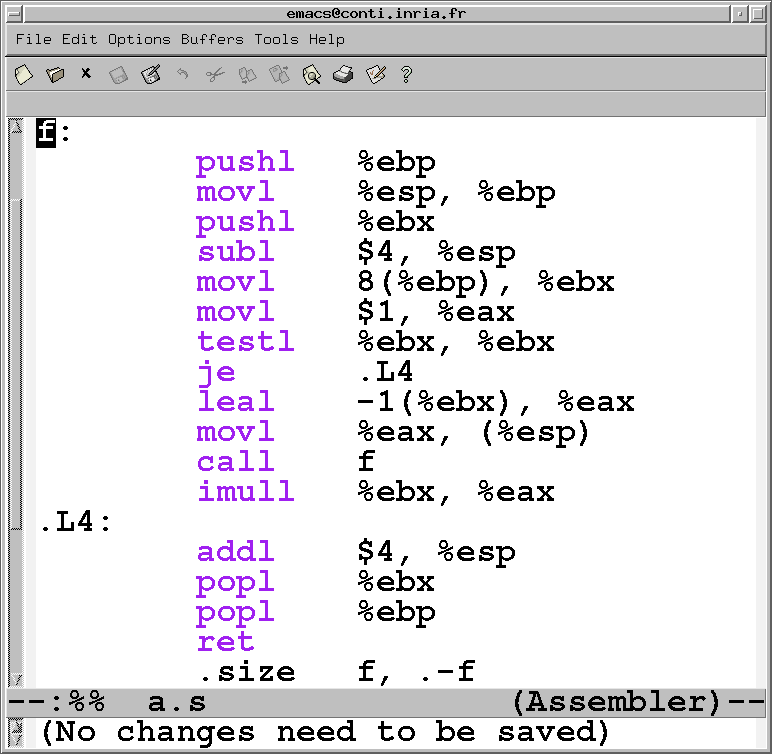Et PCF ?

Il n’existe pas d’ordinateur qui exécutent les programmes PCF directement.

Car PCF s’addresse d’abord aux être humains (sisi).

Deux techniques pour exécuter PCF.

Écrire un interpréteur, ce qui repousse le problème (dans quel langage écrire l’interpréteur ?).
Traduire PCF dans le langage de la machine, c-a-d compiler.

Machine abstraite

Traduire PCF vers une vraie machine, c’est trop compliqué.

Car la vraie machine est un peu trop simple, et il y aura des complications pour les fonctions.

À la place, nous traduisons vers une machine abstraite. Puis…

Interpréter la machine abstraite (comme Java ou ocamlc).
Ou traduire le programme de la machine abstraite vers un programme machine.
- Tout de suite (comme ocamlopt).
- Lors de l’exécution (Just In Time compilation, comme Java).

Poule et œuf

Imaginons que PCF est le seul langage L (informatique) de l’humanité, qui vient d’inventer son premier ordinateur M. Pour pouvoir exécuter un programme écrit en L, il faut :

Écrire un interpréteur I, de L, dans le langage de M.

Ensuite…

On peut écrire un compilateur de L vers M en L (plus commode qu’en M).
Compiler le compilateur (grâce à I), ce qui donne C.
On peut maintenant jeter I (mais il faut absolument garder l’exécutable C).

C’est en gros ce qui s’est passé (mais avec Fortran.)

L’écriture d’un compilateur dans son propre langage est le bootstrap (auto-amorçage).

Poule et œuf du troisième millénaire

Soit un langage informatique L déjà compilable (et bootstrapé) sur une machine M.

Je note L →^L M le source et L →^M M l’exécutable (du compilateur).

Une nouvelle machine M′ arrive sur le marché.

Changer le compilateur pour qu’il emette le code de M′, soit un nouveau compilateur L →^L M′
Le compiler, on obtient un cross-compiler L →^M M′.
Compiler L →^L M′ avec le cross-compiler.
Copier le résultat L →^M′ M′ sur M′.
À tout hasard, sur M′, compiler L →^L M′, avec L →^M′ M′, normalement on a atteint un point fixe.

Si L →^L M est buggé, il est parfois difficile de corriger.

Premiers pas

Une instruction :

Machine Un (quelques) entier sur 32/64 bits, mais qui peut se représenter symboliquement (assembleur).
movl $n %eax
Machine abstraite Un type Caml.
type ins = Ldi of int | …

L’instruction (dite load ou move immédiat) range une constante entière dans un registre.

Un registre est une case de mémoire disponible à l’intérieur de l’unité de contrôle.

Machine : un petit nombre de registres, ici %eax, %ebx…
Machine abstraite : un seul registre dit accumulateur.

Opérations arithmétiques

Inteprétation de t₁ + t₂

let rec interp … t = match t with
| Op (Add,t1,t2) ->
    let n1 = match interp … t1 with Int n -> n in
    let n2 = match interp … t2 with Int n -> n in
    Int (n1+n2)
…

Autrement dit,

Interpréter t1, ranger le résultat dans n1,
Interpréter t2, ranger le résultat dans n2,
Rendre le résultat n1+n2.

Comment faire, avec la machine qui ne connaît, ni la liaison let, ni l’appel de fonction (et encore moins l’appel récursif).

Planche : 13

Calculer avec une pile

Le code est une séquence d’instructions.

Remplacer « Interpréter t» par, executer le code qui calcule la valeur de t (dans l’accu), noté C(t).

Calculer t1, sauver l’accu dans la pile.
Calculer t2.
Additionner le contenu de l’accu et du sommet de pile (dans l’accu).

Soit compilation de t₁ + t₂.

C(t1) ; Push ; C(t2) ; Add

NB : C est la fonction de compilation, des termes PCF vers le code.

Planche : 14

Machine abstraite à pile

État de la machine : un triplet accu × pile × code, noté (A,S,C)

Accumulateur : une valeur.
Pile : suite de valeurs (en mémoire)
Code : suite d’instruction (en mémoire)

Effet des instructions : sémantique à petit pas (système de transitions).

(_, S, (Ldi n; C))	→	(n, S, C)
(A, S, (Push; C))	→	(A, (A; S), C)
(n₂, (n₁;S), (Add; C))	→	(n₁+n₂, S, C)

Le résultat du calcul est un état de la forme (n,∅,∅).

Planche : 15

Examples

Simple :

C(1+2) = Ldi 1; Push; Ldi 2; Add

Simple :

C(3+4) = Ldi 3; Push; Ldi 4; Add

Plus compliqué :

C((1+2)+(3+4)) = C(1+2); Push; C(3+4) ; Add

⎧
⎪
⎨
⎪
⎩

Ldi 1; Push; Ldi 2; Add;

Push;

Ldi 3; Push; Ldi 4; Add;

Add

À la fin, l’accumulateur contient 10 et la pile est comme au début.

Planche : 16

Machine abstraite en Caml

Types de données.
let value = Int of int | …
and stack = value list

type ins = Ldi of integer | Push | Cop of op | …
and code = ins list (* code = liste d'instructions *)
Exécution de la machine.
let rec run a s c = match a,s,c with
| _,_,(Ldi i::c) -> run (Int i) s c
| _,_,(Push::c) -> run a (a::s) c
| Int n2,(Int n1::s),(Cop Add::c) ->
run (Int (n1+n2)) s c
…
| v,[],[] -> v (* résultat final *)

Planche : 17

La pile en vrai

Il est assez facile de réaliser une pile en machine.

La mémoire est un grand tableau d’entiers, les indices sont appelés addresses.
La pile est une zone de la mémoire.
Empiler (push) le contenu de l’accumulateur :
pushl %eax
Dépiler (pop) le sommet de la pile dans l’accumulateur.
popl %eax

Si la machine donne directement les instructions push et pop.

Planche : 18

Sans instructions push/pop

L’addresse du sommet de la pile est dans un registre particulier dit pointeur de pile (%esp).

Push

subl $4,%esp
movl %eax,0(%esp)

Pop

movl 0(%esp),%eax
addl $4,%eax

Planche : 19

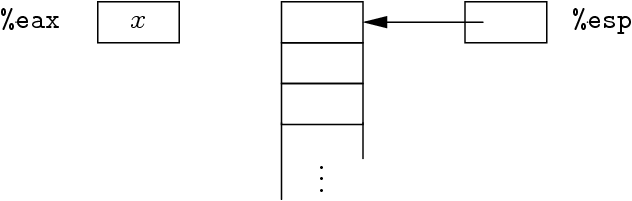
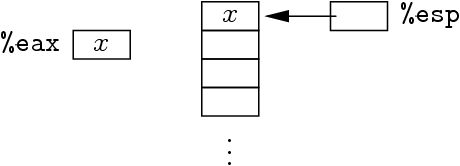
Push sur la vraie machine

État de la vraie machine :

Push :
    subl $4,%esp
    movl %eax,0(%esp)

Planche : 20

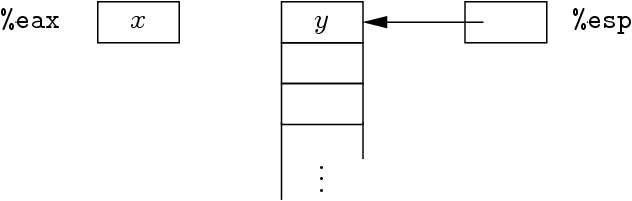
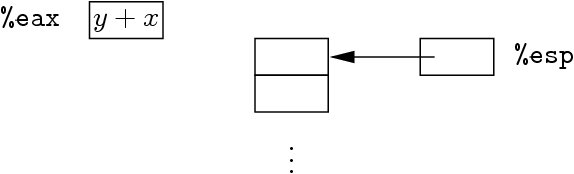
Addition en pile sur la vraie machine

Add :
  addl %eax,0(%esp)
  popl %eax

Planche : 21

Compilation

Comme une définition de la fonction C.

C(`n`)	=	Ldi n
C(t₁ op t₂)	=	C(t₁) ; Push ; C(t₂) ; Cop op

En Caml.

let rec compile t = match t with
| Num n -> [Ldi n]
| Op (op,t1,t2) -> compile t1 @ [Push] @ compile t2 @ [Cop op]
| …

Ou encore (éviter les concaténations).

let rec compile_k t k = match t with
| Num n -> Ldi i::k
| Op (op,t1,t2) -> compile_k t1 (Push::compile_k t2 (Cop op::k))

(compile t @ c = compile_k t c, pour tout terme t et tout code c)

Planche : 22

La conditionelle

Interprétation.

E ⊢ t₁↪0 E ⊢ t₂↪v

E ⊢ Ifz t₁ Then t₂ Else t₃↪v

E ⊢ t₁↪n (n ≠ 0) E ⊢ t₂↪v

E ⊢ Ifz t₁ Then t₂ Else t₃↪v

La compilation semble évidente :

Exécuter C(t₁) (le résultat est un entier dans l’accu).
- Si l’accu contient 0 alors exécuter C(t₂).
- Si l’accu contient n ≠ 0, alors exécuter C(t₃).
- Sinon, c’est une erreur (libre à nous de la détecter ou pas).

Planche : 23

Tout simplement

On se donne une instruction Test(C₂,C₃) qui va exécuter C₂ ou C₃ selon la valeur de l’accumulateur. Genre

(0,S,Test(C₂,C₃))	→	(0,S,C₂)
(n,S,Test(C₂,C₃))	→	(n,S,C₃) (n ≠0)

Et on compile :

C(Ifz t₁ Then t₂ Else t₃) = C(t₁); Test(C(t₂),C(t₃))

Planche : 24

Pas si simple

Considérer :

(Ifz t₁ Then t₂ Else t₃)+3

On aura un code du genre

C(t₁); Test(C(t₂),C(t₃)); Push; Ldi 3; Add

C’est à dire que les transitions de la machine abstraite sont plutôt :

(0,S,(Test(C₂,C₃); C)	→	(0,S,(C₂; C))
(n,S,(Test(C₂,C₃); C))	→	(n,S,(C₃; C)) (n ≠0)

Dans une implémentation Caml, on écrira malheureusement:

let rec run a s c = match a,s,c with
…
| Int 0,_,(Test (c2,c3)::c) -> run a s (c2@c)

Mais on peut éviter la concaténation avec un peu de reflexion.

Planche : 25

Conditionelle, vraie machine

Dans la vraie machine, pas de liste d’instruction en argument des instructions !

Une seule séquence, et des instructions de saut.

    C(t₁)
    testl %eax,%eax
    je L2         #Test (L2,L3)
L3:
    C(t₃)
    jmp Lk
L2:
    C(t₂)
Lk:
    pushl %eax     #Push
    movl $3,%eax   #Ldi 3
    addl 0(%esp)
    addl $4,%esp   #Add

Planche : 26

Les environnements

Les règle de la variable et du Let.

E(x) = v

E ⊢ x↪v

E ⊢ t₁↪v₁ E ⊕ [x = v₁] ⊢ t₂↪v

E ⊢ Let x = t₁ In t₂↪v

(Tiens nous sommes en appel par valeur).

On ajoute donc:

Un composant « environnement » à la machine dont l’état devient (A,S,E,C).
Une instruction Extend pour ajouter une liaison.
Une instruction Search pour trouver la valeur d’une variable.

Si Search appelle List.assoc, on a pas compilé grand chose.

Planche : 27

Retour sur les accès aux variables

Considérons :

Let x = t₁ In
Let y = t₂ In
Let z = t₃ In
t

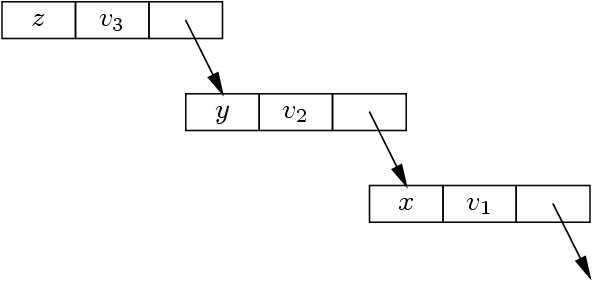
Au moment d’interpréter t, l’environnement est de de la forme :

Planche : 28

Compilation des accès aux variables

Au vu du programme la position des variables dans l’environnement à l’exécution (E) est connue (pour z, c’est 0,…, pour x c’est 2).

On peut donc simplifier E: c’est une liste de valeurs.

(A,S,E,(Extend; C))	→	(A,S,(A;E),C)
(_,S,(v₀; v₁; ⋯; v_k; ⋯),(Search k; C))	→	(v_k,S,(v₀; ⋯; v_k; ⋯),C)

Compilation, C_E(t) où E donne les positions des variables (liste de variables suffit ici).

C_E(Let x `=` t₁ In t₂)	=	C_E(t₁) ; Extend ; C_x;E(t₂)
C_{[x₀;⋯;x_k ;⋯]}(x_k)	=	Search k

Planche : 29

Mais attention

Let x = 2 In
(Let x = 1 in x+x)+x

Il faut après le code C_[x](Let x = 1 In x+x) redonner sa valeur d’origine à l’environnement.

Une solution simple est de sauver/restaurer l’environnement à l’aide de la pile S.

(A,S,E,(PushEnv; C))	→	(A,(E;S),E,C)
(A,(E;S),_,(PopEnv; C))	→	(A,S,E,C)

Et compilation complète du Let.

C_E(Let x = t₁ In t₂) = PushEnv; C_E(t₁); Extend; C_x;E(t₂); PopEnv

Planche : 30

La vraie machine

Différence essentielle entre pile et environnement :

Les cases de pile sont allouées (Push) et désallouées (Pop) explicitement. Une compilation correcte garantit que la pile est rendue comme on l’a trouvée.
Pour l’environnement, il n’est pas possible de désallouer explicitement en général (à cause des fermetures).

Il fait donc ajouter du code supplémentaire au code compilé, qui gère l’allocation mémoire (facile) et la récupération (plus dur). Ce code supplémentaire s’appelle parfois un environnement d’exécution (argl) ou encore le support à l’exécution.

Mais le principe de changer les noms de variables en positions est typique.

Planche : 31

Machine abstraite en Caml

On utilise la gestion mémoire de Caml.

let rec run a s e c = match a,s,c with
…
| _,_,(Extend::c) -> run a s (a::e) c
…

On utilise donc le support à l’exécution de Caml, sans se poser plus de questions.

Mais si on écrit une machine abstraite en assembleur (en C), il faudra se poser des questions (réponse malloc + écrire un GC).

Planche : 32

Fonctions

Interprétation de la fonction.

E ⊢ Fun x -> t↪<x•t•E>

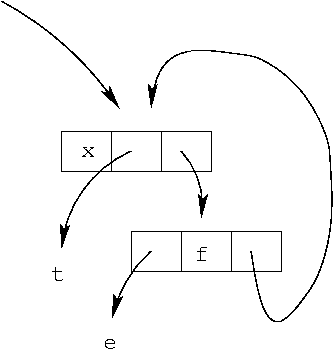
La fermeture en machine est une paire <C•E> (t compilé, et plus besoin du nom de la variable).

Par exemple :

Let y = t_y In
Let f = Fun x -> x+y In
…

La fermeture suivante représente f.

<Search 0; Push; Search 1; Add•v_y>

Planche : 33

Compilation

Une nouvelle instruction pour fabriquer les fermetures :

(_,S,E,(MakeClo [C]; C′))

→

(<C•E>,S,E,C′)

On ose à peine préciser :

let rec run a s e c = match a,s,c with
…
| _,_,(MakeClo c::c') -> run (Clo (c,e)) s e c'
…

Compilation, seuls les environnements sont (un peu) subtils.

C_E(Fun x -> t) = MakeClo [C_x;E(t)]

Noter quand même qu’une fermeture est la valeur d’une fonction, et se retrouve donc logiquement dans l’accumulateur.

Planche : 34

Application

La règle d’inteprétation.

E ⊢ t₁↪<x•t•E′> E ⊢ t₂↪v₂ E′ ⊕ [x=v₂] ⊢ t↪v

E ⊢ t₁ t₂↪v

Soit il faut :

Changer l’environnement ⇒ E′ ⊕ [x = v₂]
Interpréter t₂ dans ce nouvel environnement.

Donc une instruction Apply fait tout ça

(<C′•E′>,(v; S), E, Apply)

→

(A,∅,(v;E′),C′)

Et compilation :

C_E(t₁ t₂)

C_E(t₂); Push; C_E(t₁) ; Apply

Mais une fois de plus c’est un peu trop simple…

Planche : 35

Application en contexte

Let x = 1 In
Let f = Fun x -> x+x In
(f 2) + x

On a donc, par compilation, un code du genre:

Ldi 2; Push; Search 0; Apply; C_E(x); Add

(ou E est [f; x; ⋯])

Il faut donc retrouver l’état de la machine après le retour de la fonction.

Planche : 36

Sauver l’état de la machine, sur la pile

Un état de machine est normalement (A,S,E,C), mais

L’appel de fonction rend son résultat dans A, inutile de sauver A avant l’appel.
Si on sauve l’état sur la pile, il est bizarre de sauver la pile.
On ne sauve donc que E et C (code après apply), ce sera le travail de Apply.
(<C′•E′>,(v; S), E, (Apply; C)) → (A,(C; E; S),(v;E′),C′)
Et une règle spéciale pour la fin du code d’une fonction.
(A,(C;E;S),_,∅) → (A,S,E,C)

Planche : 37

Compilation de l’appel de fonction

Avec Apply qui sauve l’état de la machine, c’est simple.

C_E(t₁ t₂)

C_E(t₂); Push; C_E(t₁); Apply

Compte tenu de ce qui vient d’être vu, à la fin de la séquence ci dessus.

La pile S a retrouvé sa valeur du début.
L’environnement (à l’exécution) a retrouvé sa valeur du début
Et A contient la valeur rendue par la fonction.

Planche : 38

Modèle du poly

Sauvegarde et restauration explicite de l’environnement par l’appelant.

C_E(t₁ t₂) = PushEnv; C_E(t₂); Push; C_E(t₁); Apply; PopEnv

Avec un Apply moins puissant :

(A,(E;S),_,(PopEnv;C)	→	(A,S,E,C)
(<C′•E′>,(v; S), E, (Apply; C))	→	(A,S,(v;E′),(C′;C))

N.B. La compilation du poly, produit toujours Apply suivi de PopEnv.

Le modèle du poly n’a pas de règle spéciale pour le retour de fonction (mais il triche un peu dans la règle de Apply).

Planche : 39

Un miracle

Soit une fonction à deux arguments:

Let k = Fun x -> Fun y -> x+y In
k 1 2

Soit Let k = t_k In t. Le code de t_k est :

MakeClo [MakeClo [Search 1; Push; Search 0; Add]]

Son exécution construit la fermeture c = <MakeClo C•∅>, avec C = [Search 1; ⋯].

Et le code de t est :

Ldi 2; Push;

Ldi 1; Push; Search 0; Apply;

Apply;

Planche : 40

Appel de fonction à deux arguments

Au moment du premier Apply.

(<MakeClo [C]•∅>, (1;2), E, (Apply; Apply; ∅))

(Où E est l’environnement donne sa valeur à k.)

Transition Apply

(_, ((Apply; ∅); E; 2), (1;E), MakeClo C)

Exécution de MakeClo C.

(<C•(1;E)>, ((Apply; ∅); E; 2), (1;E), ∅)

Retour de fonction.

(<C•(1;E)>, (2), E, (Apply; ∅))

Nouvel Apply :

(_, ((∅);E), (2;1;E), C)

C’est à dire que le code C=[Search 1; Push; Search 0; Add] s’exécute dans l’environnement approprié (x=1 en seconde position, y=2 en première).

À la fin du code C.

(3, ((∅);E), (2;1;E), ∅)

Et retour de fonction.

(3, ∅, E, ∅)

Planche : 41

Le point fixe

Nous ne considérons que le point fixe de fonctions Fix f -> Fun x -> t.

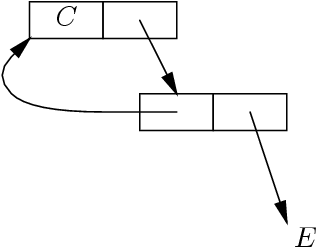
Interprétation par une fermeture bouclée.

On invente une nouvelle instruction MakeCloRec qui construit ce style de fermeture bouclée, mais pour la machine.

Avec donc la règle d’exécution :

(_,S,E,(MakeCloRec [C];C′)) → (c,S,E,C′), où c graphe c = <C•c;E>

À comparer avec :

(_,S,E,(MakeClo [C]; C′)) → (<C•E>,S,E,C′)

Planche : 42

On ose à peine préciser

Exécution en Caml.

let rec run a s e c  = match a,s,c with
…
| _,_,(MakeCloRec c::c') ->
  let rec clo_rec = Clo (c,clo_rec::e) in
  run clo_rec s e c'

Compilation, seuls les environnements sont (un peu) subtils.

C_E(Fix f -> Fun x -> t) = MakeCloRec [C_x;f;E(t)]

N.B. La transition Apply ne change pas.

Évidemment rien n’empèche de se passer de MakeClo.

C_E(Fun x -> t) = MakeCloRec [C_{x; _; E}(t)]

Planche : 43

TP, Compilateur et machine abstraite (en Caml) à deux.
La prochaine fois, PCF typé.

Planche : 44

Les transitions de la machine (A,S,E,C)

(_, S, E, (Ldi n; C))	→	(n, S, E, C)
(A, S, E, (Push; C))	→	(A, (A; S), E, C)
(n₂, (n₁;S), E, (Add; C))	→	(n₁+n₂, S, E, C)
(0,S,E,(Test(C₂,C₃);C))	→	(0,S,E,(C₂; C))
(n,S,E,(Test(C₂,C₃);C))	→	(n,S,E,(C₃; C)) (n ≠0)
(A,S,E,(Extend; C))	→	(A,S,(A;E),C)
(_,S,(v₀; v₁; ⋯; v_k; ⋯),(Search k; C))	→	(v_k,S,(v₀; ⋯; v_k; ⋯),C)
(A,S,E,(PushEnv; C))	→	(A,(E;S),E,C)
(A,(E;S),_,(PopEnv; C))	→	(A,S,E,C)

Transitions pour les fonctions

(_,S,E,(MakeClo [C]; C′))	→	(<C•E>,S,E,C′)
(_,S,E,(MakeCloRec [C];C′))	→	(c,S,E,C′), avec c = <C•c;E>
(<C′•E′>,(v; S), E, (Apply; C))	→	(A,(C; E ; S),(v;E′),C′)
(A,(C;E;S),_,∅)	→	(A,S,E,C)

État final de la machine :

(v, ∅, _, ∅)

(Pile et code vides). Le résultat est v, le contenu de l’accumulateur.

Planche : 45

Compilation de PCF

C_E(`n`)	=	Ldi n
C_E(t₁ + t₂)	=	C_E(t₁); Push; C_E(t₂); Add
C_E(Ifz t₁ Then t₂ Else t₃)	=	C_E(t₁); Test(C_E(t₂),C_E(t₃))
C_E(Let x `=` t₁ In t₂)	=	PushEnv; C_E(t₁); Extend; C_x;E(t₂); PopEnv
C_{[x₀;⋯;x_k;⋯]}(x_k)	=	Search k
C_E(t₁ t₂)	=	C_E(t₂); Push; C_E(t₁); Apply
C_E(Fun x `->` t)	=	MakeClo [C_x;E(t)]
C_E(Fix f `->` Fun x `->` t)	=	MakeCloRec [C_x;f;E(t)]

Sauf erreur, bien entendu.

Ce document a été traduit de L^AT_EX par H^EV^EA

Planche : 1

Planche : 2

Planche : 3

Presque un ordinateur

Planche : 4

Un peu plus tard (Iris 10 010, 1967)

Planche : 5

Un ordinateur

Planche : 6

Entrer un programme en mémoire

Planche : 7

Et PCF ?

Planche : 8

Machine abstraite

Planche : 9

Poule et œuf

Planche : 10

Poule et œuf du troisième millénaire

Planche : 11

Premiers pas

Planche : 12

Opérations arithmétiques

Planche : 13

Calculer avec une pile

Planche : 14

Machine abstraite à pile

Planche : 15

Examples

Planche : 16

Machine abstraite en Caml

Planche : 17

La pile en vrai

Planche : 18

Sans instructions push/pop

Planche : 19

Push sur la vraie machine

Planche : 20

Addition en pile sur la vraie machine

Planche : 21

Compilation

Planche : 22

La conditionelle

Planche : 23

Tout simplement

Planche : 24

Pas si simple

Planche : 25

Conditionelle, vraie machine

Planche : 26

Les environnements

Planche : 27

Retour sur les accès aux variables

Planche : 28

Compilation des accès aux variables

Planche : 29

Mais attention

Planche : 30

La vraie machine

Planche : 31

Machine abstraite en Caml

Planche : 32

Fonctions

Planche : 33

Compilation

Planche : 34

Application

Planche : 35

Application en contexte

Planche : 36

Sauver l’état de la machine, sur la pile

Planche : 37

Compilation de l’appel de fonction

Planche : 38

Modèle du poly

Planche : 39

Un miracle

Planche : 40

Appel de fonction à deux arguments

Planche : 41

Le point fixe