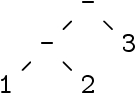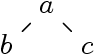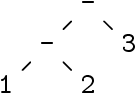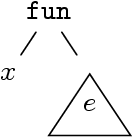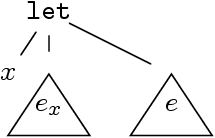Termes et relations pour la sémantique

Planche : 1

Termes et relations pour la sémantique

Objectif

La sémantique ?

Comprendre ce que fait un programme.
- Pour programmer.
- Et à plus long terme…
  - Très utile pour implémenter un langage (interpréteurs, compilateurs, analyseurs).
  - Indispensable pour prouver quoique ce soit au sujet d’un programme.
Et au passage,
- Améliorer sa connaissance de la programmation,
- (Re-)Découvrir Caml.
- Aborder les mathématiques utiles pour la sémantique.

Moyens

Deux enseignants, Luc Maranget et David Baelde.
Neuf séances, le mardi,
- Cours de 9h00 à 10h30, ici.
- TP de 10h30 à 12h30 en salle 35.
Examen (écrit — 3 heures), le 4 décembre.
Les cours préalables de Caml (mais ça c’est fait bien sûr).

Comment définir un langage de programmation ?

Une syntaxe, c’est du déjà-vu
- Spécifie les programme bien formés, « fun x -> x * x » est une expression bien formée (en Caml), mais pas « +( ».
- Outil de base pour définir la syntaxe : grammaires formelles (INF431, poly Chap. 10–12).
- Un point important : l’analyse syntaxique transforme les fichiers (suites de caractères) en arbres de syntaxe abstraite.
  
  1 - 2 - 3 →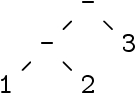
Une sémantique c’est nouveau.

Sémantique ?

Savoir que « My taylor is rich » est bien de l’anglais ne suffit pas.

Savoir que « fun x -> x * x » est bien du Caml ne suffit pas. On veut en plus savoir ce qui se passe quand on applique ce programme (cette fonction) à une entrée.

(fun x -> x * x), 4 ↪ 16

Définir la sémantique c’est définir une relation P, e ↪ v, où P est un programme (ici syntaxe abstraite), e est une entrée (ici une valeur) et v le résultat (ici une valeur).

Si à P et e donnés correspond un unique v, on définit une fonction.

Mais comment définir ↪ ? langue naturelle ou mathématiques ?

Connaître la sémantique pour programmer

Une évidence : pour bien programmer il faut savoir ce que font les programmes.

Or ce n’est pas toujours évident,

Les ordinateurs ont un comportement très précis.
Les êtres humains sont mal à l’aise devant une telle précision (non-dits, recherche de l’abstraction).

Pourtant on essaie quand même de spécifier le comportement des programmes en langue dit naturelle (français, anglais…).

Un exemple de programme

class Test {

   static int n = 0 ;

   static int f(int x, int y) { return x ; }

   static int g(int z) { n = n + z ; return n ; }

   public static void main(String [] arg) {
     System.out.println(f(g(2), g(7))) ;
   }
}

Quel est l’affichage ? « 2 », car en Java les arguments sont évalués de la gauche vers la droite, comme précisé dans la définition du langage.

Planche : 8

Autre exemple

let n = ref 0

let f x y = x

let g z = n := !n + z ; !n

let () = Printf.printf "%i\n" (f (g 2) (g 7))

Si on essaie (ranger dans test.ml et exécuter ocaml test.ml), on obtient 9.

Ici attention, la documentation de OCaml précise que l’ordre d’évaluation des arguments n’est pas spécifié.

Planche : 9

Autre exemple pertinent

let f x = let g x = x in g

let x = 3

let () = Printf.printf "%i\n" (f 1 2)

Le programme affiche : « 2 ».

On comprend un peu mieux en réécrivant :

let f y z = z

let x = 3

let () = Printf.printf "%i\n" (f 1 2)

Planche : 10

Outils dont les entrées sont des programmes

Ce sont :

les interpréteurs, les compilateurs, les analyseurs de programmes…

La sémantique est indispensable pour…

Mettre les auteurs de compilateurs/interprètes/analyseurs etc. d’accord entre eux et avec les programmeurs.
Respecter la sémantique des programmes lors des optimisations.
Prouver des propriétés des programmes rigoureusement, voire automatiquement.
Prouver les compilateurs/interprètes/analyseurs etc.

Planche : 11

Exemple de transformation de programme

Soit la fonction f :

let f x y = x

Peut-on « optimiser » tout appel f e₁ e₂ en e₁ ?

Non, car par exemple

let z = f 1 (Printf.printf "%i\n" 2 ; 2)

Mais on peut transformer :

f e₁ e₂ ⇒ let x = e₁ and y = e₂ in x

Planche : 12

La langue naturelle

Avantages :
- Tout le monde connaît (ou croit connaître).
Insuffisances :
- C’est dur d’être vraiment précis.
- Et alors, c’est souvent illisible, il faut une « culture » mal définie.
- Impossible de faire des démonstrations de théorèmes et encore moins de les automatiser.

Planche : 13

Un exemple de sémantique en langue naturelle

The while statement executes an Expression and a Statement repeatedly until the value of the Expression is false.

    WhileStatement:
            while ( Expression ) Statement

A while statement is executed by first evaluating the Expression. If the result is of type Boolean, it is subject to unboxing conversion (§5.1.8). If evaluation of the Expression or the subsequent unboxing conversion (if any) completes abruptly for some reason, the while statement completes abruptly for the same reason. Otherwise, execution continues by making a choice based on the resulting value:

If the value is true, then the contained Statement is executed. Then there is a choice:
- If execution of the Statement completes normally, then the entire while statement is executed again, beginning by re-evaluating the Expression.
- If execution of the Statement completes abruptly, see §14.12.1 below.
If the (possibly unboxed) value of the Expression is false, no further action is taken and the while statement completes normally.

If the (possibly unboxed) value of the Expression is false the first time it is evaluated, then the Statement is not executed.

La suite dans la documentation de Java.

Planche : 14

Sémantique formelle

Dans ce cours…

Nous présentons les outils qui permettent de définir la sémantique d’un langage de programmation.
Nous illustrons l’usage de ces outils en spécifiant quelques traits des langages de programmation.
Nous écrivons des programmes (interpréteur, évaluateur, vérificateur de type) dirrectement inspirés des définitions sémantiques.

Planche : 15

Relations

Planche : 16

Définition d’un ensemble (d’une relation)

Ensembles déjà connus ! ℕ, type t = int.
Constructions déjà connues : ℕ², type t = int * int.
Définition explicite :
{ x ∈ ℕ ∣ ∃ z ∈ ℕ, x = 2 × x } { (x,y) ∈ ℕ² ∣ ∃ z ∈ ℕ, x = y × z }

(Note : une relation est un sous-ensembles de paires.)
Et définition inductives…
type intlist = Nil | Cons of int * intlist

Planche : 17

Premier théorème du point fixe

E, ≤ faiblement complète :
- ≤ reflexive, antisymétrique, transitive.
- Toute suite croissante u₀, u₁, …, a une borne supérieure, notée limu_i.
E admet un minimum (noté disons ⊥).
Soit f fonction croissante et continue : f (limu_i) = limf(u_i).
Théorème : Il existe z ∈ E, tq. f(z) = z (point fixe).

Preuve : Considérer limfⁱ(⊥), c’est le plus petit point fixe de f.

Planche : 18

Preuve

Soit u_i = fⁱ(⊥).

(u_i) est croissante (u₀ = ⊥ ≤ f(⊥) = u₁ et u_i ≤ u_i+1 ⇒ u_i+1 = f(u_i) ≤ f(u_i+1) = u_i+2).
Soit p sa limite.
p est aussi la limite de (v_i)) = fⁱ⁺¹(⊥).
Donc p = limv_i = limf(u_i) = f (limu_i) = f(p) (continuité).
Et pour tout point fixe q,
- ⊥ ≤ q ⇒ u_i ≤ fⁱ(q) (croissance).
- Et donc p = limu_i ≤ limfⁱ(q) = q (def. de la borne supérieure).

Planche : 19

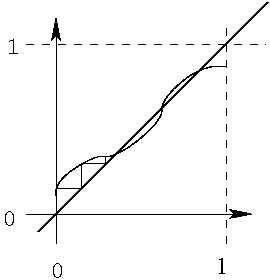
Graphiquement

[0,1], ≤ est faiblement complète.

ℝ⁺ faiblement complète ?

Planche : 20

Second théoreme du point fixe

E, ≤ fortement complète :
- Tout sous-ensemble A a une borne sup.
- Donc : tout sous-ensemble a une borne inf — Considérer la borne sup de l’ensemble des minorants de A.
Soit f croissante.
Théorème : f a un point fixe.

Preuve : la borne inférieure de C = { c ∣ f(c) ≤ c } est le plus petit point fixe de f.

Planche : 21

Preuve

Soit p borne inférieure des « contractés » C = { c ∈ E ∣ f(c) ≤ c }.

Pour tout c ∈ C,
- On a p ≤ c (p minorant de C).
- Et donc f(p) ≤ f(c) (croissance).
- Et encore f(p) ≤ c (transitivité).
- Autrement dit, f(p) minorant de C.
Soit finalement f(p) ≤ p (car p borne inf de C).
Et dans l’autre sens,
- f(f(p)) ≤ f(p) (croissance).
- Soit f(p) ∈ C.
Soit finalement p ≤ f(p) (p minorant).
Par antisymétrie, p = f(p).
Plus petit point fixe, car tous les points fixes sont dans C.

Planche : 22

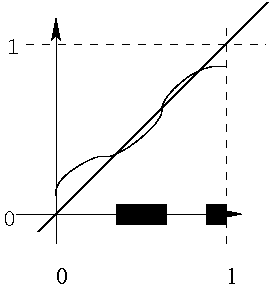
Graphiquement

[0,1], ≤ est fortement complète.

ℝ⁺ fortement complète ?

Planche : 23

Quelques exemples

Faiblement complet ? Oui (ensemble fini).
Fortement complet ? Non ? {b, c} n’a pas de borne supérieure.

Faiblement complet ? Oui.
Fortement complet ? Non ? ∅ n’a pas de borne supérieure (et {b, c} pas de borne inférieure).

Planche : 24

Exemple encore (qui va servir)

E ensemble quelconque, 2^E ensemble des parties de E.
2^E, ⊆ faiblement et fortement complet.
- Élément minimal : ∅.
- Borne sup de la collection E ? ∪_{E ∈ E} E.
- Borne inf de la collection E ? ∩_{E ∈ E} E.
f : 2^E → 2^E croissante a un point fixe.
- Plus petit point fixe : ∩_{C ∣ f(C) ⊆ C} C.
- Et si f continue : ∪_{i ∈ ℕ} fⁱ(∅).

Planche : 25

Définition inductive par l’exemple

P ensemble des entiers pairs peut être défini par les règles suivantes.

0 ∈ P

(n ∈ P ⇒ n+2 ∈ P)

Que l’on note plutôt.

0 ∈ P

n ∈ P

n+2 ∈ P

ou même

n+2

Autrement dit, P contient 0 et P est clos par la fonction n ↦ n+2.

Il est remarquable que P n’est pas le seul ensemble satisfaisant ces deux propriétés, par ex. ℕ convient.

Alors ? P est le plus petit de ces ensembles.

Planche : 26

Vérifions

Soient les fonctions f₁ : ℕ⁰ → ℕ, qui à () associe 0 ; et f₂ : ℕ → ℕ, qui à x associe x+2.

Soit ensuite F : 2^ℕ → 2^ℕ qui à X associe :

{ y ∣ y = f₁() } ⋃ { y ∣ ∃ x ∈ X, f₂(x) = y }

Soit si on veut :

F(X) = { 0 } ⋃ { x+2 ∣ x ∈ X }

F est…

Croissante, immédiat X ⊆ Y ⇒ F(X) ⊆ F(Y)).
Continue, à peine plus dur F(∪_{i ∈ N} X_i) = ∪_{i ∈ ℕ} F(X_i).
- 0 présent dans les deux ensembles.
- Sinon x = y+2 avec y ∈ X_i pour i donné.

Planche : 27

Et selon les théorèmes

Les deux règles définissent donc un ensemble d’entiers P, qui est le plus petit point fixe de F.

C’est la réunion de ∅, F(∅), F(F(∅)), soit {0, 2, 4, …}.
C’est aussi l’intersection de tous les ensembles d’entiers contenant zéro et clos par n ↦ n+2.

Et au passage P est l’ensemble des entiers pairs (2ℕ), en effet.

2ℕ est un point fixe de F, et donc P ⊆ 2N.
Si n = 2k, alors n ∈ F^k(∅) et donc n ∈ P (premier th.). Soit finalement 2ℕ ⊆ P.

Mais ce qui compte c’est que nous avons pu définir un ensemble (d’entiers) inductivement.

Planche : 28

Cas général (poly)

Pour tout ensemble E. On peut définir un sous-ensemble A de E par des fonctions f_k (eventuellement partielles) de E^n_k dans E, souvent notées comme les règles :

x₁ ⋯ x_{n_k}

f_k(x₁, …, x_{n_k})

Ce sous-ensemble est le plus petit point fixe de la fonction F de 2^E dans 2^E.

F(X) =

∪

k ∈ K

{ f_k(x₁, …, x_{n_k}) ∣ x₁, …, x_{n_k} ∈ X^n_k}

C’est aussi le plus petit ensemble clos par les règles.

Cela permet en particulier de définir des relations, qui sont des ensembles (de paires par ex.)

Planche : 29

Exemple de relation définie inductivement

Soit Σ alphabet (ensemble de caractères notés a, b)

Soit Σ^⋆ ensemble des mots (suites finies sur Σ, notés m, n).

Relation de facteur m ≼ n

є ≼ m

m ≼ m

m₁ ≼ n₁ m₂ ≼ n₂

m₁m₂ ≼ n₁n₂

m ≼ n

m ≼ n n′

m ≼ n

m ≼ n′ n

Planche : 30

Dérivation

Une dérivation ou arbre de preuve est un arbre dont les nœuds sont l’application des règles (les f_k).

L’existence d’une dérivation aboutissant en e prouve que e est dans Fⁱ(∅) (et donc dans le plus petit point fixe).

Par ex, ac ≼ abcde.

a ≼ a

c ≼ c

c ≼ cde

c ≼ bcde

ac ≼ abcde

Réciproquement, tout élément du plus petit point fixe est l’aboutissement d’une dérivation (récurrence sur i).

Planche : 31

Induction structurelle

Pour prouver une propriété P des éléments du plus petit point fixe.

Il peut suffire de montrer que P est héreditaire, c’est à dire P(x₁), …P(x_{n_k}) entraîne P(f_k(x₁,…,x_{n_k})).

Preuve L’ensemble { e ∈ E ∣ P(e) } est clos par F et second théorème.

Par ex. pour montrer que si m est un facteur de n, alors m est plus court que n :

ℓ(є) ≤ ℓ(m)

ℓ(m) ≤ ℓ(m)

ℓ(m₁) ≤ ℓ(n₁) ∧ ℓ(m₂) ≤ ℓ(n₂) ⇒ ℓ(m₁m₂) ≤ ℓ(n₁n₂)

ℓ(m) ≤ ℓ(n) ⇒ ℓ(m) ≤ ℓ(nn′)

Conséquence directe des propriétés de la longueur ℓ(є) = 0 et ℓ(m₁m₂) = ℓ(m₁) + ℓ(m₂).

Planche : 32

Autre exemple d’induction structurelle

Nous avons enfoncé une porte ouverte en prouvant que les règles

n+2

définissent bien l’ensemble des entiers pairs.

En effet, si n ∈ P alors n est pair (induction structurelle). Réciproquement, pour tout n = 2k, il existe une dérivation.

On pourrait de même enfoncer une porte (un peu moins) ouverte en démontrant que m ≼ n, ssi m est une sous-suite de n au sens usuel.

Planche : 33

Un dernier exemple

Soit une relation R, binaire, sur un ensemble E (donc un sous-ensemble du produit cartésien E × E).

On définit R^*, la fermeture reflexive et transitive de R inductivement :

e R^* e

e R e′

e R^* e

e₁ R^* e₂ e₂ R^* e₃

e₁ R^* e₃

Il est assez immédiat que

e R^* e′

⇑
⇓

∃ n ∈ ℕ, ∃ (e₁, …, e_n−1) ∈ Eⁿ⁻¹, e = e₀ R e₁ R ⋯ R e_n−1 R e_n = e′

(Induction structurelle.)

Planche : 34

Termes

Planche : 35

Insistons

Nous avons déjà dit que l’expression (Caml par ex.) « 1-2-3 » est pour nous le terme :

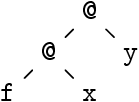
De même, nous lisons « f x y », nous comprenons (application explicitée) :

Mais sommes nous bien sûrs de savoir ce qu’est un terme ?

Planche : 36

Termes sans variables

Soit un ensemble de symboles Σ (dit signature), f, g, …
Chaque symbole est muni d’un entier, son arité, noté n_f.
Vocabulaire : Si f est d’arité zéro, c’est une constante.
L’ensemble T(Σ) des termes définis sur la signature Σ est l’ensemble d’arbres défini inductivement par les règles :

t₁ t_{n_f}

f(t₁,…,t_{n_f})

(Une règle par f de la signature.)
Où est l’arnaque ? Qu’est qu’un arbre ?
Néanmoins il semble admissible (premier théorème) qu’il s’agit de l’ensemble des arbres finis qui respectent l’arité.
Notation : On simplifie systématiquement f() en f.

Planche : 37

Exemple : expressions arithmétiques

Une infinité de constantes 0, 1, 2, …
Quatre symboles binaires +, -, *, /.

Et les expressions arithmétiques sont définies.

Une définition à peu près équivalente en Caml.

Quand on veut écrire une expression arithmétique sans dessiner un arbre, il est préférable de donner (presque) toutes les parenthèses.

t = -(-(1,2),3) ou encore t = (1-2)-3

Planche : 38

Sémantique

Définir une sémantique des expressions arithmétiques, c’est définir une relation e ↪ n entre les expressions et les entiers.

Nous donnons trois techniques.

Opérationelle à grand pas, ou naturelle : definir une relation ↪ inductivement sur la structure des expressions.
Opérationnelle à petit pas :
- Définir une étape de calcul élémentaire →.
- Définir ↪ comme →^*.
Dénotationnelle : ici peu pertinent, nous y reviendrons.

Planche : 39

Sémantique naturelle

Au symbole n on associe l’entier n, au symbole + on associe l’addition (fonction ℕ² dans ℕ, notée +)

n ↪ n

e₁ ↪ n₁ e₂ ↪ n₂

e₁ +e₂ ↪ n₁+n₂

⋯

Une trivialité, mais

let rec eval e = match e with
| Int n -> n (* NB: n et n différents *)
| Add (e1,e2) -> (* NB:  + et + différents *)
   let n1 = eval e1 and n2 = eval e2 in
   n1+n2
  …

Certes la présentation par règles d’inférences est plus neutre.

Planche : 40

Sémantique à petit pas

On définit donc la relation → sur les expressions, par une infinité d’axiomes :

0+0 → 0

0+1 → 1

1+1 → 2

⋯

Puis par huit règles d’inférence (qui ici définissent une congruence : ou peut réduire tout sous-terme).

e₁ → e′₁

e₁ +e₂ → e′ ₁ +e₂

e₂ → e′₂

e₁ +e₂ → e ₁ +e′₂

⋯

Et on pose ↪ = →^*.

Note : Les valeurs sont maintenant nécessairement un sous-ensemble des expressions.

Planche : 41

Sémantique dénotationelle

C’est une fonction des expressions dans les entiers, définie explicitement.

[[n]] = n

[[e₁ + e₂]] = [[e₁]] + [[e₂]]

Les différences avec la sémantique naturelle n’apparaissent que sur des exemples plus compliqués.

Fun x -> x+1

Est la « vraie » fonction sur ℕ, qui à x associe le successeur de x.

let rec fact n = if n <= 0 then 1 else n * fact (n-1)

Est la factorielle : 0 ↦ 1, 1 ↦ 1 × 1, 2 ↦ 2 × 1 × 1, …n ↦ n × (n−1) × ⋯ × 1 × 1, …

Planche : 42

Les variables

Comment donner une valeur à par exemple « x+x » ?

Simple ! Il suffit de remplacer x par un terme fixé. C’est la substitution [e\x].

Un premier exemple simple : expressions arithmetiques + variables.

[e\x]x = e

[e\x]y = y (y ≠ x)

[e\x](e₁ + e₂) = ([e\x]e₁) + ([e\x]e₂)

⋯

Et donc [1+1\x](x+x) = (1+1)+(1+1).

Noter : « = » et non « », c;est une meta-opération (i.e. [e_x\x]e ne fait pas partie de la syntaxe des termes).

Planche : 43

Un langage pour les fonctions

Nous avons déjà écrit par exemple n ↦ n + 2.

En Caml on écrit : « fun n -> n+2 ».

Il est remarquable que m ↦ m + 2 et fun m -> m+2 désignent la même fonction : la variable est muette.

L’expression fun x -> e, où x est une variable (ci-dessus n ou m) et e est une expression (ci-dessus n+2 ou m+2), est à comprendre comme l’arbre :

Vocabulaire : On dit que la construction fun lie la variable x dans la sous-expression e. L’occurence de x dans e est ici libre.

Planche : 44

Autres constructions liantes

Un autre exemple (Caml) est « let x = e_x in e », à lire comme :

où x est liée dans le sous-terme e.

Considérer aussi : « let rec x = e_x in e », où x est liée dans e_x et e.

Planche : 45

Expressions arithmétiques + variables

Une expression e est :

Une variable,
Ou une constante entière { 0,1, … }.
L’application d’une opération e₁ + e₂ etc.
Une liaison let x = e_x in e.

Dans let x = e_x in e, x est liée dans e.

Planche : 46

Variables d’une expression

Définies par induction sur la structure des expressions.

V(0) = ∅

⋯

V(x) = { x }

V(e₁ +e₂) = V(e₁) ⋃ V(e₂)

V(let x = e_x in e) = { x } ⋃ V(e_x) ⋃ V(e)

module VarSet =
  Set.Make
    (struct type t = var let compare = … end)

let rec vars e = match e with
| Int _ -> VarSet.empty
| Add (e1,e2) | Sub (e1,e2) | Mul (e1,e2) | Div (e1,e2) ->
    VarSet.union (vars e1) (vars e2)
| Var x -> VarSet.singleton x
| Let (x,ex,e) ->
    VarSet.add (VarSet.union (vars ex) (vars e)) x

Planche : 47

Variables libres

Ce sont les variables non-liées, c’est-à-dire celles dont la valeur doit être fournie.

F(`x+1`)	=	{ `x` }
F(`x+1+y`)	=	{ `x`, `y` }
F(`let x = 1 in x+1`)	=	∅
F(`let x = 1 in x+1+y`)	=	{ `y` }

F(0) = ∅

⋯

F(x) = { x }

F(e₁ +e₂) = F(e₁) ⋃ F(e₂)

F(let x = e_x in e) = V(e_x) ⋃

⎛
⎝

V(e) ∖ { x }

⎞
⎠

Et aussi,

F(fun x -> e) = F(e) ∖ { x }

Planche : 48

Calcul des variables libres

Planche : 49

Sémantique naturelle des expressions avec variables

Une expression peut maintenant contenir des variables (libres).

Il faut connaître la valeur d’une variable libre.
Pour la remplacer par cette valeur.

Une solution simple : l’environnement. La relation sémantique est maintenant de la forme

Γ ⊢ e ↪ v

Où ici,

Γ est un environnement, c’est à dire une fonction (de domaine fini) des variables dans les valeurs.
e est une expression.
v est une valeur, ici un entier.

Planche : 50

Sémantique des expressions avec variables

Γ ⊢ n ↪ n

Γ(x) = n

Γ ⊢ x ↪ n

Γ ⊢ e₁ ↪ n₁ Γ ⊢ e₂ ↪ n₂

Γ ⊢ e₁ + e₂ ↪ n₁ + n₂

⋯

Planche : 51

Programmation

Un environnement est une liste de paires x × v.

type env = (var * int) list

let rec assoc x env = match env with
| [] -> raise Not_found
| (y,vy)::env ->
   if x=y then vy
   else assoc x env
(* Disponible comme List.assoc *)

let rec eval env e = match e with
| Var x -> assoc x env
| Let (x,ex,e) ->
    let vx = eval env ex in
    eval ((x,vx)::env) e
| … (* Comme avant ou presque *)

Planche : 52

Vers la sémantique à petit pas

Comment définir → (une étape de calcul) sur un terme qui contient let ? L’idée est que on peut effectuer la liason let x = e_x in e en remplaçant x par e_x dans e.

Une substitution est tout simplement une fonction (de domaine fini) des variables dans les… termes. On note [e_x\x] la substitution qui à x associe e_x.

Les substitutions sont des morphismes, c-à-d respectent la structure de terme.

Les substitutions s’appliquent aux variables libres seulement :

[`2`\`x`] (`x+1`)	=	`2+1`
[`2`\`x`] (fun `x -> x+1`)	=	fun `x -> x+1`
[`2`\`x`] (let `x = x+x` in `x`)	=	let `x = 2+2` in `x`

Planche : 53

Définition de la substitution, premier essai

Remplacer les variables libres par leurs définitions :

[e\x]0 = 0

⋯

[e\x]x = e

[e\x]y = y

[e\x]e₁ + e₂ = [e\x]e₁ + [e\x]e₂

[e\x](let x = e₁ in e₂) = let x = [e\x]e₁ in e₂

[e\x](let y = e₁ in e₂) = let y = [e\x]e₁ in [e\x]e₂

Et de même :

[e\x](fun x -> e₁) = fun x -> e₁

[e\x](fun y -> e₁) = fun y -> [e\x]e₁

Planche : 54

Mais attention

Il semble donc que l’on puisse réduire let x = e_x in e en [e_x\x] (e).

Soit la fonction qui ajoute y libre à son argumemt.

fun x -> x + y

Sous-expression par exemple de :

let y = e_y in fun x -> x + y

En substituant…

Si e_y est 4 on a fun x -> x + 4.
Si e_y est z on a fun x -> x + z.
Si e_y est x a-t-on ? fun x -> x + x ?
Il ne vaut meux pas ! Considérer :
let x = 1 in let y = x in fun x -> x + y

Planche : 55

Alpha-équivalence

Dans l’exemple [x\y](fun x -> x+y), nous sommes victimes de la capture de la variable libre x, qui devient liée en traversant la liaison fun x -> …

Si l’argument de la fonction est nommé z on peut substituer :
[x\y](fun z -> z + y) = fun z -> z + x.
Les fonctions fun x -> x + y et fun z -> z + y sont les mêmes (changement de la variable muette).

L’alpha-équivalence est l’égalité modulo le changement des variables muettes.

Planche : 56

Une définition possible de la substitution

En évitant les captures.

[e\x](let x = e₁ in e₂) = let x = [e\x]e₁ in e₂

[e\x](let y = e₁ in e₂) = let z = [e_x\x]e₁ in [e_x\x]([z\y]e₂)

Où z ci-dessus n’appartient ni à F(e_x), ni à F(e₂).

C’est bien compliqué.

Planche : 57

Programmer la substitution

En pratique : z est une variable « fraiche », c’est à dire une variable nouvelle.

type var = int

let fresh_var =
  let count = ref 0 in
  fun () ->
    let v = !count in
    count := !count+1 ;
    v

let rec subst x ex e = match e with
| Int _ -> e
| Add (e1,e2) -> Add (subst x ex e1, subst x ex e2)
  … (* Sub, etc. idem *)
| Var y ->  if x = y then ex else e
  …

Planche : 58

Programmer la substitution, cas délicat

| Let (y, ey, e) ->
    if x=y then
      Let (y, subst x ex ey, e)
    else
      let z = fresh_var () in
      Let (z, subst x ex ey, subst x ex  (subst y (Var z) e))

Pas le plus efficace, certainement… Mais suffisant pour définir le calcul sur le let.

Pour définir une étape de calcul, il reste à

Choisir un sous-terme réductible (un redex)
Et à le remplacer par son réduit.

Planche : 59

En TP

Un peu de Caml (ensembles).
Un peu de termes.
Et calcul d’un point fixe.

Ce document a été traduit de L^AT_EX par H^EV^EA

Planche : 1

Planche : 2

Objectif

Planche : 3

Moyens

Planche : 4

Comment définir un langage de programmation ?

Planche : 5

Sémantique ?

Planche : 6

Connaître la sémantique pour programmer

Planche : 7

Un exemple de programme

Planche : 8

Autre exemple

Planche : 9

Autre exemple pertinent

Planche : 10

Outils dont les entrées sont des programmes

Planche : 11

Exemple de transformation de programme

Planche : 12

La langue naturelle

Planche : 13

Un exemple de sémantique en langue naturelle

Planche : 14

Sémantique formelle

Planche : 15

Planche : 16

Définition d’un ensemble (d’une relation)

Planche : 17

Premier théorème du point fixe

Planche : 18

Preuve

Planche : 19

Graphiquement

Planche : 20

Second théoreme du point fixe

Planche : 21

Preuve

Planche : 22

Graphiquement

Planche : 23

Quelques exemples

Planche : 24

Exemple encore (qui va servir)

Planche : 25

Définition inductive par l’exemple

Planche : 26

Vérifions

Planche : 27

Et selon les théorèmes

Planche : 28

Cas général (poly)

Planche : 29

Exemple de relation définie inductivement

Planche : 30

Dérivation

Planche : 31

Induction structurelle

Planche : 32

Autre exemple d’induction structurelle

Planche : 33

Un dernier exemple

Planche : 34

Planche : 35

Insistons

Planche : 36

Termes sans variables

Planche : 37

Exemple : expressions arithmétiques

Planche : 38

Sémantique

Planche : 39

Sémantique naturelle

Planche : 40

Sémantique à petit pas

Planche : 41

Sémantique dénotationelle

Planche : 42